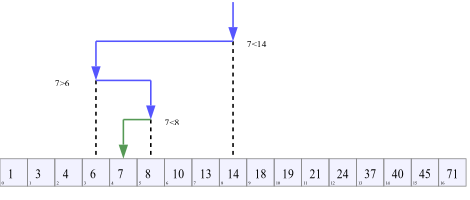
배열이 정렬되어 있거나, 정렬해도 시간이 더 추가되지 않으면 이진 검색을 써야 한다. O(n)이 O(logn)으로 줄기 때문이다. 문제는 목표 값이 배열에 없거나, 중복된 값이 있을 경우이다. 이를 위해 이진 검색을 크게 3개로 나눠보겠다.
- 그냥: 목표 값의 아무데나 찾음
- 하한(lower bound): 목표 값의 제일 작은 곳을 찾음
- 상한(upper bound): 목표 값의 제일 큰 곳을 찾음
int binarySearch(int[] arr, int target) {
int l = 0, r = arr.length - 1;
while (l <= r) {
int m = (l + r) >>> 1;
if (arr[m] > target) r = m - 1;
else if (arr[m] < target) l = m + 1;
else return m;
}
return l;
}
int lowerBound(int[] arr, int target) {
int l = 0, r = arr.length - 1;
while (l <= r) {
int m = (l + r) >>> 1;
if (arr[m] >= target) r = m - 1;
else l = m + 1;
}
return l;
}
int upperBound(int[] arr, int target) {
int l = 0, r = arr.length - 1;
while (l < r) {
int m = (l + r) >>> 1;
if (arr[m] > target) r = m;
else l = m + 1;
}
return l;
}
예를 들어 배열이 0 1 2 3 5 5 5 10 이고 목표 값이 5라면, 그냥 이진 검색은 여러 5 중에서 아무거나 찾고, 하한은 가장 왼쪽의 5, 상한은 가장 오른쪽의 5의 다음 칸을 찾는다. 다만 10을 찾는다면 10의 다음 칸이 없으니까 10을 가리킨다.
그러면 목표 값이 존재하지 않으면 어떡할까? 예를 들어 위의 배열에서 목표 값이 4라면, 3와 5 사이의 칸, 즉 5를 가리킬 것이다. 이것은 insertion sort를 할 때 insertion point와 같다.
그런데 11을 찾는다면 어떨까? 11의 insertion point는 10의 다음이므로 배열을 벗어나는 칸이 된다. 그런데, 일반 이진검색과 하한에서는 이 insertion point를 돌려주지만 상한은 오히려 배열의 범위를 벗어나지 않고 10의 위치를 돌려주니까 이것을 조심해야 한다.
int[] arr = new int[]{0,1,2,3,5,5,5,10};
System.out.println(binarySearch(arr, 5)); // 5
System.out.println(lowerBound(arr, 5)); // 4
System.out.println(upperBound(arr, 5)); // 7
System.out.println(binarySearch(arr, 4)); // 4
System.out.println(lowerBound(arr, 4)); // 4
System.out.println(upperBound(arr, 4)); // 4
System.out.println(binarySearch(arr, 3)); // 3
System.out.println(lowerBound(arr, 3)); // 3
System.out.println(upperBound(arr, 3)); // 4
System.out.println(binarySearch(arr, 10)); // 7
System.out.println(lowerBound(arr, 10)); // 7
System.out.println(upperBound(arr, 10)); // 7
System.out.println(binarySearch(arr, 11)); // 8
System.out.println(lowerBound(arr, 11)); // 8
System.out.println(upperBound(arr, 11)); // 7참고로 배열의 왼쪽과 오른쪽 인덱스의 가운데 값을 찾을 때, 그냥 (l + r) / 2 를 하면 배열이 매우 클 경우 overflow가 날 수 있다. 이를 방지하기 위해서 l + (r – l) / 2 를 하거나, 아니면 어차피 인덱스는 모두 0 이상이므로 overflow가 나던 말던 일단 더한 다음에, 부호를 상관하지 않고 오른쪽으로 shift를 한 칸 하면 2로 나눈 것과 같아진다. (l + r) >>> 1 이것은 JDK의 Arrays.binarySearch0() 을 참고했다.
![]()